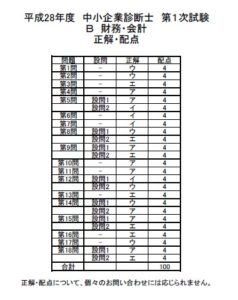
第16問
年後の配当は 105 千円、その後毎年3%の成長が永続することを見込んでい
る。割引率-株主資本コスト/が年5%である場合、配当割引モデルに基づく企業価値の推定値として最も適切なものはどれか。
ア 1,575 千円
イ 2,100 千円
ウ 3,500 千円
エ 5,250 千円
第16問 エ 解説
配当割引モデル(一定成長モデル)に関する計算問題である。 基本的な知識で解答で きる。 必ず正解したい。
配当割引モデルとは、 株主に対する直接的な支払額である配当金額を基準としてを算定する方法である。 配当金額=CIFと考え、期待利回り(=株主資本コスト) 割り引くことで株価を求める。
株価 で このモデル
には、配当金が毎年一定額のゼロ成長モデルと、一定の割合で配当金が増 えていく一定成長モデルがある。 これらの公式は、以下のとおりである。
〈ゼロ成長モデル)
1株当たり配当金額
株価=
期待利回り (株主資本コスト)
〈一定成長モデル〉 1年後の1株当たり配当金額 株価= 期待利回り (株主資本コスト) 一配当成長率
本問では、1年後の配当(105千円)や配当成長率(3%)が与えられていることから、 一定成長モデルの公式を用いる。
また、問われているのが、株価ではなく、企業価値である点に注意する。企業価値は 負債価値と株主価値を合計したものであるが、本問では負債価値が与えられていないの で、株主価値を計算すればよい。株主価値は、株式時価総額(=株価×発行済株式総数) で表すことができる。
そこで、一定成長モデルの公式から、株主価値を求める式に変形する。1株当たり配 当金額は配当金額を発行済株式総数で除した金額なので、公式の両辺に発行済株式総数
を掛けると、
株価×発行済株式総数(株主価値 ×
1年後の配当金額 発行済株式総数
×発行済株式総数 期待利回り株主資本コスト)一配当成長率
株主価値
1年後の配当金額
期待利回り(株主資本コスト)一配当成長率 と変形できる。この式に与えられた数値を代入すると、
株主価値%3D 1年後の配当金額105 株主資本コスト0.05 配当成長率0.03 %3D35,250(千円)
と求められる。 よって、エが正解である。 が
過去翻出同时
平成26年度第20間(設問3) 平成23年度第20間設問2)
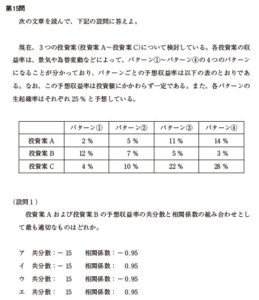

第15問
次の文章を読んで、下記の設問に答えよ。
現在、3つの投資案-投資案 A〜投資案 Cについて検討している。各投資案の収益率は、景気や為替変動などによって、パターン①〜パターン④の4つのパターンになることが分かっており、パターンごとの予想収益率は以下の表のとおりであ
る。なお、この予想収益率は投資額にかかわらず一定である。また、各パターンの生起確率はそれぞれ 25 % と予想している。
パターン① パターン② パターン③ パターン④
投資案 A 2 % 5 % 11 % 14 %
投資案 B 12 % 7 % 5 % 3 %
投資案 C 4 % 10 % 22 % 28 %
(設問1)
投資案 A および投資案 B の予想収益率の共分散と相関係数の組み合わせとし
て最も適切なものはどれか。
ア 共分散:-15 相関係数:-0.95
イ 共分散:-15 相関係数: 0.95
ウ 共分散: 15 相関係数:-0.95
エ 共分散: 15 相関係数: 0.95
(設問2)
投資案 A および投資案 C に関する記述として最も適切なものはどれか。
ア 投資案 A と投資案 C に半額ずつ投資する場合も、投資案 C のみに全額投資する場合も、予想収益率の分散は同じである。
イ 投資案 A の予想収益率と投資案 C の予想収益率の相関係数は2である。
ウ 投資案 C の予想収益率の期待値は 64 % である。
エ 投資案 C の予想収益率の標準偏差は、投資案 A の予想収益率の標準偏差の2倍である。

投資案のパターンごとの予想収益率に関する問題である。 まず、各投資案の予想収益率の期待値を計算する。 パターン①から率を組入比率 (25%) で加重平均すると、 投資案Aの予想収益率の期待値= (2 + 5 + 11 + 14) × 0.25
④までの予想収益
<-8 (%)
投資案Bの予想収益率の期待値=(12 +7 +5 +3) x 0.25
第15問
<= 6.75 (%)
投資案Cの予想収益率の期待値= (4 + 10 + 22 +28) × 0.25
= 16 (%)
とそれぞれ求められる。
(設問1) ア
共分散と相関係数の特徴がわかれば、選択肢を絞ることができる。 時間の許す範囲で 取り組もう。 投資案AとBの共分散と相関係数の公式は以下のとおりである。
投資案AとBの共分散=状況①の (投資案Aの偏差×投資案Bの偏差×発生確率)
+状況② の (投資案Aの偏差×投資案Bの偏差X発生確率)
+状況③ の (投資案Aの偏差X投資案Bの偏差発生確率) +状況④の (投資案Aの偏差×投資案Bの偏差×発生確率)
投資案AとBの相関係数=
投資案Aと投資案Bの共分散
投資案Aの標準偏差×投資案Bの標準偏差
電卓を使用できない本試験で、これらの公式を使って、 共分散や相関係数の値を計算 した受験者は皆無であったと思われる。 本間では、これらの計算をしなくても、各投資 案の予想収益率の期待値とその差の符号がわかれば正答できる。 各投資案の差と生起確率は以下のとおり整理できる。
パターン① 投資案A 投資案B 投資案C 2-8-6 (%) 5-8--3 (%) 11-8-3 (%) 12-6.75=5.25(%) 7-6.75=0.25(%) 5-675--1.75(%) 3-6.75-3.75(%) 14-8-6 (%) 4-16-12 (%) 10-16=-6(%) 22-166 (%) 28-16-12 (%) 0.25 0,25 0.25 0.25
共分散は、パターンごとに投資案AとBそれぞれの偏差と発生確率を掛けてから、 そ れらを足し合わせて計算する。 投資案AとBそれぞれの偏差はすべて符号が逆なので、 共分散の符号は、必ずマイナスになる。
また、標準偏差は分散の平方根をとった値なので必ず符号はプラスとなる。 よって、 共分散の符号がマイナスであれば、相関係数の符号はマイナスとなる。 以上より、 共分散と相関係数の符号がともにマイナスのアが正解である。 なお、投資案AとBの共分散と相関係数の値を計算した場合は以下のとおりである。 投資案AとBの共分散の計算は、 投資案AとBの共分散
|= (-6) × 5.25+(-3) × 0.25 +3×(-1.75) +6 × (-3.75) × 0.25 = 15
となる。
また、投資案AおよびBの分散と標準偏差の計算は、 投資案Aの分散=(-6)^2+(-3)^ + 3' + 6 × 0.25 22.5 投資案A の標準偏差=22.54.743 投資案Bの分散= 15.25" + 0.252+(-1.75)+(-3.75) x 0.25 = 11.1875
投資Bの標準偏差=11,1875 3.344
よって、 投資案AとBの相関係数の計算は、
投資案AとBの相関係数
投資案Aと投資案Bの共分散-15
投資案Aの標準偏差 4.743 × 投資案Bの標準偏差 3.344 -0.95
(設問2) エ
各投資案の予想収益率の期待値と分散相関係数の特徴がわかれば、誤りの選択肢は 除外できる。 消去法を活用して、選択肢を絞りたい。 ア 不適切である。 実際に両者の分散を求めてみよう。 まず、投資案Aと投資案Cに半額 ずつ投資する場合、 予想収益率および期待収益率は次のようになる。
7.5% 16.5% 21% 12% & 投資案 C
※パターン① (2+4)+2-3(%)
パターン②:15 +10)÷2=7.5 (%)
A-7@: (11+22)+2=165 (%)
-20 (14+28) +2=21 (%)
期待収益率 (3+7.5 + 16.5 +21) × 0.25-12
したがって、 分散は
(%)
1(3-12)²+(7.5-12)+(16.5-12)+(21-12)³ × 0.25
(81+20.25 +20.25 +81) x 0.25
= 50.625
と求められる。
一方、 投資案Cの期待収益率は、
期待収益率= (4 + 10 + 22 + 28) × 0.25
= 16 (%)
となるため、分散は下記のとおり計算できる。
-(4-16)+(10-16)+(22-16)+(2816) × 0.25
(144 +36 +36 +144) x 0.25
<= 90
よって、両者の分散は異なる。
イ不適切である。 相関係数は、必ず-1から1までの値をとる。 不適切である。 先に計算したとおり、投資案Cの予想収益率の期待値は16%である。 エ最も適切である。 投資案AとCのパターンごとの予想収益率を比べると、 投資案Cは
投資案Aの
2倍になっていることがわかる。 そこで、投資案Cの分散の計算式を投資案 Aの分散に置き換えられないか、検討する。 投資案Cの分散の計算式を整理すると、 1(4-16)+(10-16)+(22-16)+(28-16) × 0.25 =[12 (2-8)1 +12 (5-8)1²+12 (11-8)1²+12 (148)2] x 0.25 = 2² 1(2-8)1²+(5-8) + (11-8) +(148)²1 x 0.25 =4×投資案Aの分散
となり、投資案投資案Cの標準偏差 =√4×投資案Aの分散
Aの分散を4倍したものが投資案Cの分散になることがわかる。また、 標準偏差は分散の平方根をとった値なので、
=2×投資案Aの標準偏差
となり、 投資案Cの標準偏差は投資案Aの2倍となる。
解テク
電卓を使用できない本試験で、工の標準偏差の値を計算した受験者は皆無であったと 思われる。やみくもに標準偏差の計算に時間をかけるべきでない。 本間は選択肢アから ウを検討して、消去法で解答すべき問題である。
過去類出問題
平成27年度 第17間 平成26年度 第17 平成24年度 第19


第14問
加重平均資本コストWACCの計算手順に関する次の記述について、下記の設問に答えよ。
加重平均資本コストは、株主資本-自己資本/コストと他人資本コストを、その
A に応じて加重平均することで求められる。加重平均に用いるのは、理論的にはそれぞれの B である。
また、他人資本コストには C を考慮する必要がある。具体的には、他人
資本コストに D を乗じることで、 C を考慮した他人資本コストを
求める。
(設問1)
記述中の空欄AおよびBにあてはまる語句の組み合わせとして最も適切なものはどれか。
ア A:運用形態 B:時価
イ A:運用形態 B:簿価
ウ A:資本構成 B:時価
エ A:資本構成 B:簿価
オ A:調達源泉 B:簿価
(設問2)
記述中の空欄CおよびDにあてはまる語句の組み合わせとして最も適切なもの
はどれか。
ア C:節税効果 D: 1-限界税率
イ C:節税効果 D:限界税率
ウ C:レバレッジ効果 D: 1-限界税率
エ C:レバレッジ効果 D: 1+限界税率
オ C:レバレッジ効果 D:限界税率

加重平均資本コスト (WACC) の計算手順に関する問題である。 基本的な答できる。必ず正解したい。
加重平均資本コストは、以下の計算式で求める。
WACC=
E
x株主資本コスト+ E+D
知識で解
D
x負債コストX (1-t)
E+D
※ 株主資本 (白己資本) の時価. D 負債(他人資本)の時価、t税率
この計算式に基づいて、 空欄に当てはまる語句の組合せを選択する。 1) ウ
加重平均資本コストの計算には、 株主資本 (自己資本) と負債 (他人資本) の時価の 資本構成 (割合) を用いる。 よって、空欄 A は「資本構成」 空欄 Bは「時 価」 となる。
(設問2) ア
他人資本、 すなわち負債には節税効果があるので、 加重平均資本コストの計算には税 引後の他人資本コストを用いる。 よって,空欄 C ] は 「節税効果」 空欄 [ D は 「1-限界税率」となる。
過去出問題
平成27年度 第14問 平成25年度 第14問 平成24年度 第16間 平成23年度 第16
(
第14問

第13問
企業買収に関する略語の説明として最も適切なものはどれか。
ア KPI とは、同業他社の株価を参照することを通じて買収価格を決定したうえで、経営権の取得等を行うことである。
イ LBO とは、従業員が資金を出し合って、経営権の取得等を行うことである。
ウ MBO とは、金融機関が自身の資金によって経営権の取得等を行うことである。
エ TOB とは、不特定多数の者に対し、証券市場以外の場における株券の買付け等の勧誘を通じて経営権の取得等を行うことである。

第13問 エ
企業買収に関する略語の問題である。 テキストが押さえられていれば、イ、ウが誤り で工が正答だと気付くはずである。 これを機に、解けるようにしておきたい ア 不適切である。 KPIは、 Key Performance Indicators の略である。 組織や事業 業 務の目標の達成度合いを測る定量的な指標のことで、重要業績評価指標などと訳される。 イ不適切である。 LBOは、 Leveraged Buy-Out の略である。 買収対象企業の資産や将 来キャッシュ・フローを担保として借入金を調達し、その資金で経営権の取得等を行う ことである。 なお、 従業員が資金を出し合っ
て、 経営権の取得等を行うことをEBO (Employee Buy-Out) という。 ウ不適切である。 MBO
は、Management Buy-Out の略である。 企業の経営陣が株主か ら自社の株式を譲り受けて、経営権の取得等を行うことである。 エ最も適切である。 TOBは、 Take-Over Bid の略である。 不特定多数の株主から証券 市場外で株式等を買い集める行為である。 企業買収や子会社化など、 第三者が対象企業 の経営権の取得等を目的に実施することが多い。


第12問
資本資産評価モデルCAPMに関する下記の設問に答えよ。
(設問1)
資本資産評価モデルを前提とした場合の記述として、最も適切なものはどれ か。
ア β=-1である資産を安全資産と呼ぷ。
イ β=1であるリスク資産の期待収益率は、市場ボートフォリオの期侍収益率と同じである。
ウ β=2であるリスク資産の予想収益率の分散は、β=1であるリスク資産の予想収益率の分散の2倍である。
エ 市場ポートフォリオのリターンが正のとき、β=0.5であるリスク資産の価格が下落することはない。
(設問2)
資本資産評価モデルを前提とした場合、以下の資料に基づく株式の期待収益率として最も適切なものを、下記の解答群から選べ。
資 料
市場ポートフォリオの期待収益率:8 %
無リスク資産の期待収益率:3 %
β:1.4
実効税率:40 %
解答群
ア 4.4 %
イ 7 %
ウ 10 %
エ 11.2 %

第 12 問 解説
資本資産評価モデル (CAPM)に関する問題である。 本園では、 CAPM理論の公式を使いこなせれば解答できる。 CAPM理論の公式は 以下のとおりである。
個別証券の期待収益率
=リスク・フリー・レート
+個別証券のβx (市場ポートフォリオの期待収益率ーリスク・フリー・レート)
(設問1) イ
試算が必要になるが、 CAPM理論の公式に当てはめれば正答できる。 これを機に、 解けるようにしておきたい。
ア 不適切である。 8=0である資産を安全資産と呼ぶ。 8 (ベータ) は、 市場全体の収 益率の動き (市場動向) に対し、個別証券 (リスク資産) の収益率がどれだけ動くかを 表す値である。 安全資産の期待収益率は、リスク・フリー・レートという一定の値であ り、市場動向の影響をまったく受けない。したがって、安全資産の8は0である。 なお、 =-1の個別証券は、市場ポートフォリオと正反対の動きをする。 イ 最も適切である。 CAPM理論の公式にβ=1 を代入すると、 個別証券の期待収益率
フリー・レート +市場ボートフォリオの期待収益率ーリスク・フリー・レート 市場ポートフォリオの期待収益率 となり、 個別証券の期待収益率と市場ポートフォリオの期待収益率は一致する。 不適切である。 8の
=リスク・
ウ 公式は、以下のとおりである。
p×個のα B
市の
※p (ロー) 個別証券と市場ポートフォリオの相関係数 個の。 (シグマ) 個別証券の標準偏差 市の。 (シグマ) 市場ポートフォリオの標準偏差
個別証券 (リスク資産) の分散を求めるには、この公式の両辺を2乗すればよい。
2×個の
市の
-
x個別証券の分散
市場ポートフォリオの分散
この両辺に、
市場ポートフォリオの分散
P
個別証券の分散=
を掛けると、
市場ポートフォリオの分散×B2
P
と変形できる。 この式に、 β=1 を代入すると、
個別証券の分散
市場ボートフォリオの分散×1
P
となる。 同様に、β=2 を代入すると、
個別証券の分散=
市場ポートフォリオの分散
となる。これらを比較すると、 β=2のときの分散はβ=1のときの4倍となる。 エ 不適切である。 B は、 個別証券 (リスク資産) の価格の動きの大きさが市場ポートフォ リオの価格の動きに比べて大きいか小さいかを示す指標である。 が 0.5 というのは、 リスク資産の価格が市場ポートフォリオの価格の動きの5割方、小さく動く傾向がある ことを意味している。 小さいとはいえ、価格が動くということは、価格が上昇したり下 落したりすることなので、 下落しないとはいえない。
テク
選択肢ウは検討に時間がかかるので、 先に他の選択肢を検討すべき問題である (選択 肢イが正しいと判断できれば、選択肢ウを検討する必要はない)。 (設問2) ウ
CAPM理論の公式を利用した計算問題である。 基本的な知識で解答できるので、 必 ず正解したい。 【資料】 の数値をCAPM理論の公式に当てはめると、次のようになる。 株式の期待収益率
=無リスク資産の期待収益率3% +81.4
× (市場ポートフォリオの期待収益率 8%-無リスク資産の期待収益率3%) = 10 (%)
よって、 ウが正解である。
変動性 (リスク) 確実に押さえておきたい。
B 収益率の変動性(リスク) 市場ポートフォリオよりも個別証券のほうが大きい a=1 市場ボートフォリオと同じ 0