

第12問
資本資産評価モデルCAPMに関する下記の設問に答えよ。
(設問1)
資本資産評価モデルを前提とした場合の記述として、最も適切なものはどれ か。
ア β=-1である資産を安全資産と呼ぷ。
イ β=1であるリスク資産の期待収益率は、市場ボートフォリオの期侍収益率と同じである。
ウ β=2であるリスク資産の予想収益率の分散は、β=1であるリスク資産の予想収益率の分散の2倍である。
エ 市場ポートフォリオのリターンが正のとき、β=0.5であるリスク資産の価格が下落することはない。
(設問2)
資本資産評価モデルを前提とした場合、以下の資料に基づく株式の期待収益率として最も適切なものを、下記の解答群から選べ。
資 料
市場ポートフォリオの期待収益率:8 %
無リスク資産の期待収益率:3 %
β:1.4
実効税率:40 %
解答群
ア 4.4 %
イ 7 %
ウ 10 %
エ 11.2 %
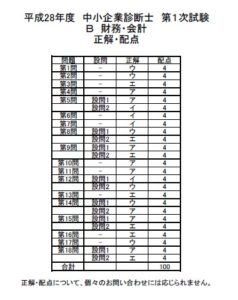
第 12 問 解説
資本資産評価モデル (CAPM)に関する問題である。 本園では、 CAPM理論の公式を使いこなせれば解答できる。 CAPM理論の公式は 以下のとおりである。
個別証券の期待収益率
=リスク・フリー・レート
+個別証券のβx (市場ポートフォリオの期待収益率ーリスク・フリー・レート)
(設問1) イ
試算が必要になるが、 CAPM理論の公式に当てはめれば正答できる。 これを機に、 解けるようにしておきたい。
ア 不適切である。 8=0である資産を安全資産と呼ぶ。 8 (ベータ) は、 市場全体の収 益率の動き (市場動向) に対し、個別証券 (リスク資産) の収益率がどれだけ動くかを 表す値である。 安全資産の期待収益率は、リスク・フリー・レートという一定の値であ り、市場動向の影響をまったく受けない。したがって、安全資産の8は0である。 なお、 =-1の個別証券は、市場ポートフォリオと正反対の動きをする。 イ 最も適切である。 CAPM理論の公式にβ=1 を代入すると、 個別証券の期待収益率
フリー・レート +市場ボートフォリオの期待収益率ーリスク・フリー・レート 市場ポートフォリオの期待収益率 となり、 個別証券の期待収益率と市場ポートフォリオの期待収益率は一致する。 不適切である。 8の
=リスク・
ウ 公式は、以下のとおりである。
p×個のα B
市の
※p (ロー) 個別証券と市場ポートフォリオの相関係数 個の。 (シグマ) 個別証券の標準偏差 市の。 (シグマ) 市場ポートフォリオの標準偏差
個別証券 (リスク資産) の分散を求めるには、この公式の両辺を2乗すればよい。
2×個の
市の
-
x個別証券の分散
市場ポートフォリオの分散
この両辺に、
市場ポートフォリオの分散
P
個別証券の分散=
を掛けると、
市場ポートフォリオの分散×B2
P
と変形できる。 この式に、 β=1 を代入すると、
個別証券の分散
市場ボートフォリオの分散×1
P
となる。 同様に、β=2 を代入すると、
個別証券の分散=
市場ポートフォリオの分散
となる。これらを比較すると、 β=2のときの分散はβ=1のときの4倍となる。 エ 不適切である。 B は、 個別証券 (リスク資産) の価格の動きの大きさが市場ポートフォ リオの価格の動きに比べて大きいか小さいかを示す指標である。 が 0.5 というのは、 リスク資産の価格が市場ポートフォリオの価格の動きの5割方、小さく動く傾向がある ことを意味している。 小さいとはいえ、価格が動くということは、価格が上昇したり下 落したりすることなので、 下落しないとはいえない。
テク
選択肢ウは検討に時間がかかるので、 先に他の選択肢を検討すべき問題である (選択 肢イが正しいと判断できれば、選択肢ウを検討する必要はない)。 (設問2) ウ
CAPM理論の公式を利用した計算問題である。 基本的な知識で解答できるので、 必 ず正解したい。 【資料】 の数値をCAPM理論の公式に当てはめると、次のようになる。 株式の期待収益率
=無リスク資産の期待収益率3% +81.4
× (市場ポートフォリオの期待収益率 8%-無リスク資産の期待収益率3%) = 10 (%)
よって、 ウが正解である。
変動性 (リスク) 確実に押さえておきたい。
B 収益率の変動性(リスク) 市場ポートフォリオよりも個別証券のほうが大きい a=1 市場ボートフォリオと同じ 0




コメントフォーム