
第15問
次の文章を読んで、下記の設問に答えよ。
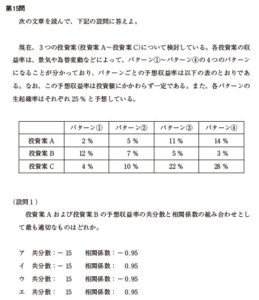
現在、3つの投資案-投資案 A〜投資案 Cについて検討している。各投資案の収益率は、景気や為替変動などによって、パターン①〜パターン④の4つのパターンになることが分かっており、パターンごとの予想収益率は以下の表のとおりであ
る。なお、この予想収益率は投資額にかかわらず一定である。また、各パターンの生起確率はそれぞれ 25 % と予想している。
パターン① パターン② パターン③ パターン④
投資案 A 2 % 5 % 11 % 14 %
投資案 B 12 % 7 % 5 % 3 %
投資案 C 4 % 10 % 22 % 28 %
(設問1)
投資案 A および投資案 B の予想収益率の共分散と相関係数の組み合わせとし
て最も適切なものはどれか。
ア 共分散:-15 相関係数:-0.95
イ 共分散:-15 相関係数: 0.95
ウ 共分散: 15 相関係数:-0.95
エ 共分散: 15 相関係数: 0.95
(設問2)
投資案 A および投資案 C に関する記述として最も適切なものはどれか。
ア 投資案 A と投資案 C に半額ずつ投資する場合も、投資案 C のみに全額投資する場合も、予想収益率の分散は同じである。
イ 投資案 A の予想収益率と投資案 C の予想収益率の相関係数は2である。
ウ 投資案 C の予想収益率の期待値は 64 % である。
エ 投資案 C の予想収益率の標準偏差は、投資案 A の予想収益率の標準偏差の2倍である。
投資案のパターンごとの予想収益率に関する問題である。 まず、各投資案の予想収益率の期待値を計算する。 パターン①から率を組入比率 (25%) で加重平均すると、 投資案Aの予想収益率の期待値= (2 + 5 + 11 + 14) × 0.25
④までの予想収益
<-8 (%)
投資案Bの予想収益率の期待値=(12 +7 +5 +3) x 0.25
第15問
<= 6.75 (%)
投資案Cの予想収益率の期待値= (4 + 10 + 22 +28) × 0.25
= 16 (%)
とそれぞれ求められる。
(設問1) ア
共分散と相関係数の特徴がわかれば、選択肢を絞ることができる。 時間の許す範囲で 取り組もう。 投資案AとBの共分散と相関係数の公式は以下のとおりである。
投資案AとBの共分散=状況①の (投資案Aの偏差×投資案Bの偏差×発生確率)
+状況② の (投資案Aの偏差×投資案Bの偏差X発生確率)
+状況③ の (投資案Aの偏差X投資案Bの偏差発生確率) +状況④の (投資案Aの偏差×投資案Bの偏差×発生確率)
投資案AとBの相関係数=
投資案Aと投資案Bの共分散
投資案Aの標準偏差×投資案Bの標準偏差
電卓を使用できない本試験で、これらの公式を使って、 共分散や相関係数の値を計算 した受験者は皆無であったと思われる。 本間では、これらの計算をしなくても、各投資 案の予想収益率の期待値とその差の符号がわかれば正答できる。 各投資案の差と生起確率は以下のとおり整理できる。
パターン① 投資案A 投資案B 投資案C 2-8-6 (%) 5-8--3 (%) 11-8-3 (%) 12-6.75=5.25(%) 7-6.75=0.25(%) 5-675--1.75(%) 3-6.75-3.75(%) 14-8-6 (%) 4-16-12 (%) 10-16=-6(%) 22-166 (%) 28-16-12 (%) 0.25 0,25 0.25 0.25
共分散は、パターンごとに投資案AとBそれぞれの偏差と発生確率を掛けてから、 そ れらを足し合わせて計算する。 投資案AとBそれぞれの偏差はすべて符号が逆なので、 共分散の符号は、必ずマイナスになる。
また、標準偏差は分散の平方根をとった値なので必ず符号はプラスとなる。 よって、 共分散の符号がマイナスであれば、相関係数の符号はマイナスとなる。 以上より、 共分散と相関係数の符号がともにマイナスのアが正解である。 なお、投資案AとBの共分散と相関係数の値を計算した場合は以下のとおりである。 投資案AとBの共分散の計算は、 投資案AとBの共分散
|= (-6) × 5.25+(-3) × 0.25 +3×(-1.75) +6 × (-3.75) × 0.25 = 15
となる。
また、投資案AおよびBの分散と標準偏差の計算は、 投資案Aの分散=(-6)^2+(-3)^ + 3' + 6 × 0.25 22.5 投資案A の標準偏差=22.54.743 投資案Bの分散= 15.25" + 0.252+(-1.75)+(-3.75) x 0.25 = 11.1875
投資Bの標準偏差=11,1875 3.344
よって、 投資案AとBの相関係数の計算は、
投資案AとBの相関係数
投資案Aと投資案Bの共分散-15
投資案Aの標準偏差 4.743 × 投資案Bの標準偏差 3.344 -0.95
(設問2) エ
各投資案の予想収益率の期待値と分散相関係数の特徴がわかれば、誤りの選択肢は 除外できる。 消去法を活用して、選択肢を絞りたい。 ア 不適切である。 実際に両者の分散を求めてみよう。 まず、投資案Aと投資案Cに半額 ずつ投資する場合、 予想収益率および期待収益率は次のようになる。
7.5% 16.5% 21% 12% & 投資案 C
※パターン① (2+4)+2-3(%)
パターン②:15 +10)÷2=7.5 (%)
A-7@: (11+22)+2=165 (%)
-20 (14+28) +2=21 (%)
期待収益率 (3+7.5 + 16.5 +21) × 0.25-12
したがって、 分散は
(%)
1(3-12)²+(7.5-12)+(16.5-12)+(21-12)³ × 0.25
(81+20.25 +20.25 +81) x 0.25
= 50.625
と求められる。
一方、 投資案Cの期待収益率は、
期待収益率= (4 + 10 + 22 + 28) × 0.25
= 16 (%)
となるため、分散は下記のとおり計算できる。
-(4-16)+(10-16)+(22-16)+(2816) × 0.25
(144 +36 +36 +144) x 0.25
<= 90
よって、両者の分散は異なる。
イ不適切である。 相関係数は、必ず-1から1までの値をとる。 不適切である。 先に計算したとおり、投資案Cの予想収益率の期待値は16%である。 エ最も適切である。 投資案AとCのパターンごとの予想収益率を比べると、 投資案Cは
投資案Aの
2倍になっていることがわかる。 そこで、投資案Cの分散の計算式を投資案 Aの分散に置き換えられないか、検討する。 投資案Cの分散の計算式を整理すると、 1(4-16)+(10-16)+(22-16)+(28-16) × 0.25 =[12 (2-8)1 +12 (5-8)1²+12 (11-8)1²+12 (148)2] x 0.25 = 2² 1(2-8)1²+(5-8) + (11-8) +(148)²1 x 0.25 =4×投資案Aの分散
となり、投資案投資案Cの標準偏差 =√4×投資案Aの分散
Aの分散を4倍したものが投資案Cの分散になることがわかる。また、 標準偏差は分散の平方根をとった値なので、
=2×投資案Aの標準偏差
となり、 投資案Cの標準偏差は投資案Aの2倍となる。
解テク
電卓を使用できない本試験で、工の標準偏差の値を計算した受験者は皆無であったと 思われる。やみくもに標準偏差の計算に時間をかけるべきでない。 本間は選択肢アから ウを検討して、消去法で解答すべき問題である。
過去類出問題
平成27年度 第17間 平成26年度 第17 平成24年度 第19




コメントフォーム