第2問
本支店会計において本店集中計算制度を採用している場合、A 支店から B 支店
へ現金 200,000 円を送付したときの B 支店の仕訳として、最も適切なものはどれ
か。
ア 借B 支店 200,000 貸A 支店 200,000
イ 借現 金 200,000
ウ 借現 金 200,000
貸A 支店 200,000
貸B 支店 200,000
エ 借現 金 200,000 貸本 店 200,000
正答率 44.2%
第2問 【解答】
本問は、企業会計の基礎企業結合)の分野の「本支店会計(本店集中制度)」に関す る問題である。
本支店会計において、支店が複数ある場合、支店相互間の取引について、支店分散計算 削度と本店集中計算語度の2つの会計処理方法がある。
【解説】
本店集中計算制度では、支店相互間の取引はすべて本店を経由して取引されたものとみなして処理される。各支店では、取引相手の支店名を用いず本店定に記録し、本店では、 支店相互間の取引の報告を受けた際に各支店名を付した支店断定により記録する。 支店分散計算制度は、各支店において取引相手の支店名を用いた支店樹定で記録する方 法である。ただし、この方法だと、本店が支店相互間の取引を管理学できないため、本 店集中計算制度を採用するのが一般的である。
本問の取引について、各方法により仕訳をすると次の通りである。 《本店集中普算制度。
<A支店>(借)本 200,000 <日支店>惜)現 200.000 (貸)本 <本店> (借)B 200.000 (資)A200.000 200,000
<支店分散計算制度>
支店
200,000
<A支店> (借)B支店 200,000 (貸)現 <B支店> 200,000 200,000 200,000
よって、エが正解である。

第1問
以下の資料に基づいて、今期の売上原価として最も適切なものを下記の解答群か
ら選べ。
資 料
期首商品棚卸高
当期商品純仕入高
期末帳簿棚卸数量
期末実地棚卸数量
120,000 円
650,000 円
1,300 個原価@100 円
1,000 個
棚卸減耗損は売上原価とする。
解答群
ア 610,000 円
イ 640,000 円
ウ 670,000 円
エ 700,000 円

【解説】
正答率 68.2 96
本間は、簿記の基礎(費用の会計)の分野の「売上原」に関する計算問題である。 売上原価とは、当期の売上高に対応する販売した商品にかかった原を表し、「期首商 品卸高+当期商品仕入高一期末商品川高」で計算する。また、本間において、設問内 に「知摩耗損は売上原価とする」とあることに注意する必要がある。 まず、期末棚卸高と棚卸摩耗損を計算する。
期末実施期卸高
= 100 19 X 1,300=130.00019
機抑耗損
%3D100円×(1,300-1,000個)%3D30,000円
本問のような売上原価を求める問題の場合、次のようなBOX図を書くと分かりやすい。 の,
BOX 期首商品棚卸高 120, 000 9 当期商品範仕入額」 84.000 売上原価 650.000 加減耗損 670,000 30,000 期末実施棚卸高 (棚卸摩耗損を除く) 100.000 19
第1問 【解答]
Box図より、売上原価は以下式により求めることができることがわかる。
売上原価一期首商品棚卸高+当期商品純仕入高一(期末実施棚卸高一機毛根) 棚卸印形
上記式に与えられたと算出した値を代入する。 売上原価=120,000円+650,000円-(130,000円-30,000円) =670,000 よって、ウが正解である。

第18問
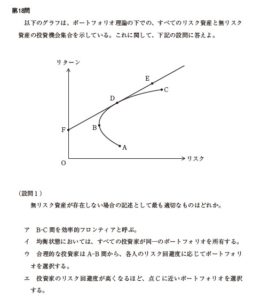
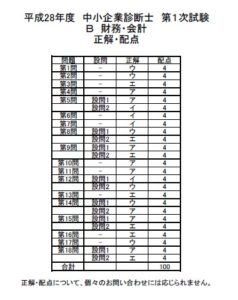
以下のグラフは、ポートフォリオ理論の下での、すべてのリスク資産と無リスク資産の投資機会集合を示している。これに関して、下記の設問に答えよ。
(設問1)
/
無リスク資産が存在しない場合の記述として最も適切なものはどれか。
ア B-C 間を効率的フロンティアと呼ぶ。
イ 均衡状態においては、すべての投資家が同一のポートフォリオを所有する。
ウ 合理的な投資家は A-B 間から、各人のリスク回避度に応じてポートフォリ
オを選択する。
エ 投資家のリスク回避度が高くなるほど、点 C に近いポートフォリオを選択
する。
(設問2)
無リスク資産が存在する場合の記述として最も適切なものはどれか。
ア 均衡状態においては、すべての投資家が所有する危険資産と無リスク資産の
比率は同じである。
イ 資金の借り入れが、無リスク資産利子率において無制限に可能である場合、
投資家は D-E 間を選択せず、F-D 間から各自のリスク回避度に応じてポート
フォリオを選択する。
ウ すべてのリスク回避的な投資家は無リスク資産のみに投資する。
エ 点 D を選択する投資家も存在する。
第18問
ボートフォリオ理論に基づく、無リスク資産の有無に応じた投資機会集合に関する間 題である。グラフの直線や曲線が何を示しているかがわかれば解答できるので、同様の 問題が出題された場合には必ず解けるようにしておきたい。 ポートフォリオとは、証券などの資産を複数組み合わせたものである。無リスク資産 は、安全資産ともよばれ、リスクを冒さずにリターンを得られる資産である。
- 184 -
一般的には、国債が安全資産の例として取り上げられる。
●解答・解説編
一方、リスク資産は危険資産ともよばれ、無リスク資産よりも高い収益が期待される が元本割れのおそれもある資産である。たとえば、株式、投資信託、外貨預金などがあ
グラフを示すと以下のようになる。
無リスク資とリスク資産がある 場合の効率的フロンティア
D
リスク資産のみの場合 の効率的フロンティア
無リスク資産 のみの場合の
上図のとおり、点Fは無リスク資産のみの場合の効率的フロンティア、F-D間およ びその延長線上は無リスク資産とリスク資産がある場合の効率的フロンティア、B-C 間はリスク資産のみの場合の効率的フロンティアをそれぞれ示している。
無リスク資産が存在しない場合、すなわち、リスク資産のみの場合を検討すればよい。 ア最も適切である。B-C間は、リスク資産のみの場合の効率的フロンティアを示して いる。効率的フロンティアとは、投資機会集合のうち、同一のリスクに対してリターン が最大となる点の集合のことである。
イ不適切である。すべての投資家の需要とすべてのリスク資産の供給が一致した均衡状 態であっても、投資家ごとにリスク回避度は異なるので、同一のポートフォリオを所有 するとは限らない。
つ不適切である。合理的な投資家であれば、D-B間と同程度のリスクにもかかわらず リターンが低いA-B間を選択しない。合理的な投資家は各人のリスク回避度に応じて リターンが最大となるB-C間(リスク資産のみの場合の効率的フロンティア)からガー トフォリオを選択する。
工不適切である。点Cはリスクが最も高い点である。投資家のリスク回避度が高くなる のであれば、リスクが高いボートフォリオを選択しない。
(設問2) エ
無リスク資産が存在する場合、すなわち、無リスク資産のみの場合と無リスク資産と リスク資産がある場合を検討すればよい。
ア不適切である。すべての投資家の需要とすべての資産の供給が一致した均衡状態で あっても、投資家ごとのリスク回避度は異なるので、危険資産と無リスク資産の所有比
Tom
率が同じとは限らない。
イ不適切である。資金の借り入れが無リスク資産利子率で無制限に可能な場合には、巨 Dから点Eを通る直線上の任意のポートフォリオを選択する。資金の借り入れができな い場合には、F-D間の任意のボートフォリオを選択する。 り
不適切である。リスク回避的な投資家は各人のリスク回避度に応じて、点F、D、E を通る直線上から任意のポートフォリオを選択するので、無リスク資産のみに投資する 点Fとは限らない。 エ最も適切
である。点Dは無リスク資産とリスク資産がある場合の効率的フロンティア 上にあるので、この点を選択する投資家も存在する。
三國
平成27年度第18間、第19問
●今後の学習対策・
「財務・会計」合格への最短ルートは、管理会計とファイナンスの分野で確実に得点 することである。
「財務・会計」の科目合格率は、昨年度~今年度と2年続けて高く、来年度は強化の 可能性がある。ただし、難易度を大きく左右しているのは財務会計で、テキストに掲載 されていない論点が多数出題される場合である。管理会計、ファイナンスの難易度は、 それほど変わらない。また、管理会計、ファイナンスは財務会計に比べて出題範囲が狭 いにもかかわらず、試験問題の約70%を占めている。したがって、合格にはこれら2 分野の攻略が必要不可欠である。
余裕がある受験者は、財務会計の知識を深めてもよいが、日商簿記検定などの他資格 の勉強をするのは遠回りになりかねない。それをするくらいなら、テキストや問題集の 内容を自分の言葉で説明できるようになろう。論理的に説明する力がつけば、ひねった 問題が出題されても対応できるし、2次試験対策もスムーズに進むはずだ。 「財務・会計」は計算問題が多く、時間制約の厳しい科目でもある。
それでも、「計算 問題は3分以内、理論問題は1分以内」というように、自分なりの制限時間を設ければ、 60分で完答することは可能である。毎回時間を通って、過去問題集に取り組もう。

第17問
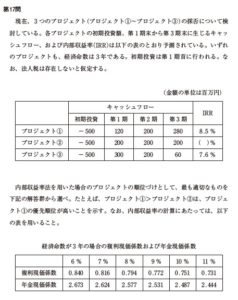
現在、3つのプロジェクト-プロジェクト①〜プロジェクト③/の採否について検討している。各プロジェクトの初期投資額、第1期末から第3期末に生じるキャッシュフロー、および内部収益率-IRR/は以下の表のとおり予測されている。いずれ
のプロジェクトも、経済命数は3年である。初期投資は第1期首に行われる。なお、法人税は存在しないと仮定する。
-金額の単位は百万円/
キャッシュフロー
IRR初期投資 第1期 第2期 第3期
プロジェクト① - 500 120 200 280 8.5 %
プロジェクト② - 500 200 200 200 - /%
プロジェクト③ - 500 300 200 60 7.6 %
内部収益率法を用いた場合のプロジェクトの順位づけとして、最も適切なものを
下記の解答群から選べ。たとえば、プロジェクト①>プロジェクト②は、プロジェ
クト①の優先順位が高いことを示す。なお、内部収益率の計算にあたっては、以下
の表を用いること。
経済命数が3年の場合の複利現価係数および年金現価係数
6% 7% 8% 9% 10% 11%
複利現価係数 0.840 0.816 0.794 0.772 0.751 0.731
年金現価係数 2.673 2.624 2.577 2.531 2.487 2.444
解答群
ア プロジェクト①>プロジェクト②>プロジェクト③
イ プロジェクト①>プロジェクト③>プロジェクト②
ウ プロジェクト②>プロジェクト①>プロジェクト③
エ プロジェクト②>プロジェクト③>プロジェクト①
オ プロジェクト③>プロジェクト①>プロジェクト②

第17問 解説
内部収益率法(IRR法)に基づいてプロジェクトを順位づけする問題である。内部 収益率法の計算結果から現価係数表を読み取れれば正答できる問題である。 内部収益率法の公式は以下のとおりである。
内部収益率法(IRR法)
TAR:将来の正味CFの割引現在価値合計一初期投資額%3D0となるような割引率 採否:1RR(内部収益率)>資本コスト(要求利益率)→採用 IRR(内部収益率)く資本コスト(要求利益率)→不採用 ※複数の投資案を順位づけする場合には、IRRが大きな投資案ほど望ましい
本、 本問では、複数のプロジェクトの順位づけが問われている。そこで、まずプロジェクト①とプロジェクト
②のIRRを比べると、プロジェクト①のIRR>プロジェクトの のIRRとなるので、前者のほうが有利であり、「解答群)はア、イ、ウに絞られる。 次に、プロジェクトのIRRを求める。プロジェクト②の第1期から第3期まで のキャッシュフローは同額(200百万円)であることから、年金現価係数を用いる。 IRRの計算式より、
将来の正味CFの割引現在価値合計一初期投資額(500百万円)=0 200百万円×年金現価係数-500百万円=30 となる。これを年金現価係数の式に変形すると、
500 年金現価係数D = 2.5 200
2.5は、年金現価係数表をみると、9%(2.531)と10%(2487)の間の 値であることがわかる。このため、プロジェクト②のIRRは、9%と10%の間となる。 よって、プロジェクト②のIRRが最も大きいので、「プロジェクトのプロジェク ト①>プロジェクトの」のウが正解である。
となる。この
ココッ出る!!
さまざまな投資の意思決定方法について、それぞれ採用基準を覚えておきたい。
投資の意思決定方法 正味現在価値法 (NPVA 投資案の採用基準 正味現在価値がプラスであれば採用 「内部利益資本コスト(要求利益」であれば採用 内部利益 (IRR法) 回収期間法 投資利率法 「同期間く会社の定める基準年度」であれば採用 「投資会社の定める基準利益率」であれ
過去頻出問題
ば採用
平成26年度第16間 平成25年度第17問 間 平成24年度第18問

第16問
年後の配当は 105 千円、その後毎年3%の成長が永続することを見込んでい
る。割引率-株主資本コスト/が年5%である場合、配当割引モデルに基づく企業価値の推定値として最も適切なものはどれか。
ア 1,575 千円
イ 2,100 千円
ウ 3,500 千円
エ 5,250 千円

第16問 エ 解説
配当割引モデル(一定成長モデル)に関する計算問題である。 基本的な知識で解答で きる。 必ず正解したい。
配当割引モデルとは、 株主に対する直接的な支払額である配当金額を基準としてを算定する方法である。 配当金額=CIFと考え、期待利回り(=株主資本コスト) 割り引くことで株価を求める。
株価 で このモデル
には、配当金が毎年一定額のゼロ成長モデルと、一定の割合で配当金が増 えていく一定成長モデルがある。 これらの公式は、以下のとおりである。
〈ゼロ成長モデル)
1株当たり配当金額
株価=
期待利回り (株主資本コスト)
〈一定成長モデル〉 1年後の1株当たり配当金額 株価= 期待利回り (株主資本コスト) 一配当成長率
本問では、1年後の配当(105千円)や配当成長率(3%)が与えられていることから、 一定成長モデルの公式を用いる。
また、問われているのが、株価ではなく、企業価値である点に注意する。企業価値は 負債価値と株主価値を合計したものであるが、本問では負債価値が与えられていないの で、株主価値を計算すればよい。株主価値は、株式時価総額(=株価×発行済株式総数) で表すことができる。
そこで、一定成長モデルの公式から、株主価値を求める式に変形する。1株当たり配 当金額は配当金額を発行済株式総数で除した金額なので、公式の両辺に発行済株式総数
を掛けると、
株価×発行済株式総数(株主価値 ×
1年後の配当金額 発行済株式総数
×発行済株式総数 期待利回り株主資本コスト)一配当成長率
株主価値
1年後の配当金額
期待利回り(株主資本コスト)一配当成長率 と変形できる。この式に与えられた数値を代入すると、
株主価値%3D 1年後の配当金額105 株主資本コスト0.05 配当成長率0.03 %3D35,250(千円)
と求められる。 よって、エが正解である。 が
過去翻出同时
平成26年度第20間(設問3) 平成23年度第20間設問2)

第15問
次の文章を読んで、下記の設問に答えよ。
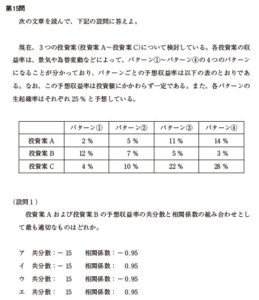
現在、3つの投資案-投資案 A〜投資案 Cについて検討している。各投資案の収益率は、景気や為替変動などによって、パターン①〜パターン④の4つのパターンになることが分かっており、パターンごとの予想収益率は以下の表のとおりであ
る。なお、この予想収益率は投資額にかかわらず一定である。また、各パターンの生起確率はそれぞれ 25 % と予想している。
パターン① パターン② パターン③ パターン④
投資案 A 2 % 5 % 11 % 14 %
投資案 B 12 % 7 % 5 % 3 %
投資案 C 4 % 10 % 22 % 28 %
(設問1)
投資案 A および投資案 B の予想収益率の共分散と相関係数の組み合わせとし
て最も適切なものはどれか。
ア 共分散:-15 相関係数:-0.95
イ 共分散:-15 相関係数: 0.95
ウ 共分散: 15 相関係数:-0.95
エ 共分散: 15 相関係数: 0.95
(設問2)
投資案 A および投資案 C に関する記述として最も適切なものはどれか。
ア 投資案 A と投資案 C に半額ずつ投資する場合も、投資案 C のみに全額投資する場合も、予想収益率の分散は同じである。
イ 投資案 A の予想収益率と投資案 C の予想収益率の相関係数は2である。
ウ 投資案 C の予想収益率の期待値は 64 % である。
エ 投資案 C の予想収益率の標準偏差は、投資案 A の予想収益率の標準偏差の2倍である。

投資案のパターンごとの予想収益率に関する問題である。 まず、各投資案の予想収益率の期待値を計算する。 パターン①から率を組入比率 (25%) で加重平均すると、 投資案Aの予想収益率の期待値= (2 + 5 + 11 + 14) × 0.25
④までの予想収益
<-8 (%)
投資案Bの予想収益率の期待値=(12 +7 +5 +3) x 0.25
第15問
<= 6.75 (%)
投資案Cの予想収益率の期待値= (4 + 10 + 22 +28) × 0.25
= 16 (%)
とそれぞれ求められる。
(設問1) ア
共分散と相関係数の特徴がわかれば、選択肢を絞ることができる。 時間の許す範囲で 取り組もう。 投資案AとBの共分散と相関係数の公式は以下のとおりである。
投資案AとBの共分散=状況①の (投資案Aの偏差×投資案Bの偏差×発生確率)
+状況② の (投資案Aの偏差×投資案Bの偏差X発生確率)
+状況③ の (投資案Aの偏差X投資案Bの偏差発生確率) +状況④の (投資案Aの偏差×投資案Bの偏差×発生確率)
投資案AとBの相関係数=
投資案Aと投資案Bの共分散
投資案Aの標準偏差×投資案Bの標準偏差
電卓を使用できない本試験で、これらの公式を使って、 共分散や相関係数の値を計算 した受験者は皆無であったと思われる。 本間では、これらの計算をしなくても、各投資 案の予想収益率の期待値とその差の符号がわかれば正答できる。 各投資案の差と生起確率は以下のとおり整理できる。
パターン① 投資案A 投資案B 投資案C 2-8-6 (%) 5-8--3 (%) 11-8-3 (%) 12-6.75=5.25(%) 7-6.75=0.25(%) 5-675--1.75(%) 3-6.75-3.75(%) 14-8-6 (%) 4-16-12 (%) 10-16=-6(%) 22-166 (%) 28-16-12 (%) 0.25 0,25 0.25 0.25
共分散は、パターンごとに投資案AとBそれぞれの偏差と発生確率を掛けてから、 そ れらを足し合わせて計算する。 投資案AとBそれぞれの偏差はすべて符号が逆なので、 共分散の符号は、必ずマイナスになる。
また、標準偏差は分散の平方根をとった値なので必ず符号はプラスとなる。 よって、 共分散の符号がマイナスであれば、相関係数の符号はマイナスとなる。 以上より、 共分散と相関係数の符号がともにマイナスのアが正解である。 なお、投資案AとBの共分散と相関係数の値を計算した場合は以下のとおりである。 投資案AとBの共分散の計算は、 投資案AとBの共分散
|= (-6) × 5.25+(-3) × 0.25 +3×(-1.75) +6 × (-3.75) × 0.25 = 15
となる。
また、投資案AおよびBの分散と標準偏差の計算は、 投資案Aの分散=(-6)^2+(-3)^ + 3' + 6 × 0.25 22.5 投資案A の標準偏差=22.54.743 投資案Bの分散= 15.25" + 0.252+(-1.75)+(-3.75) x 0.25 = 11.1875
投資Bの標準偏差=11,1875 3.344
よって、 投資案AとBの相関係数の計算は、
投資案AとBの相関係数
投資案Aと投資案Bの共分散-15
投資案Aの標準偏差 4.743 × 投資案Bの標準偏差 3.344 -0.95
(設問2) エ
各投資案の予想収益率の期待値と分散相関係数の特徴がわかれば、誤りの選択肢は 除外できる。 消去法を活用して、選択肢を絞りたい。 ア 不適切である。 実際に両者の分散を求めてみよう。 まず、投資案Aと投資案Cに半額 ずつ投資する場合、 予想収益率および期待収益率は次のようになる。
7.5% 16.5% 21% 12% & 投資案 C
※パターン① (2+4)+2-3(%)
パターン②:15 +10)÷2=7.5 (%)
A-7@: (11+22)+2=165 (%)
-20 (14+28) +2=21 (%)
期待収益率 (3+7.5 + 16.5 +21) × 0.25-12
したがって、 分散は
(%)
1(3-12)²+(7.5-12)+(16.5-12)+(21-12)³ × 0.25
(81+20.25 +20.25 +81) x 0.25
= 50.625
と求められる。
一方、 投資案Cの期待収益率は、
期待収益率= (4 + 10 + 22 + 28) × 0.25
= 16 (%)
となるため、分散は下記のとおり計算できる。
-(4-16)+(10-16)+(22-16)+(2816) × 0.25
(144 +36 +36 +144) x 0.25
<= 90
よって、両者の分散は異なる。
イ不適切である。 相関係数は、必ず-1から1までの値をとる。 不適切である。 先に計算したとおり、投資案Cの予想収益率の期待値は16%である。 エ最も適切である。 投資案AとCのパターンごとの予想収益率を比べると、 投資案Cは
投資案Aの
2倍になっていることがわかる。 そこで、投資案Cの分散の計算式を投資案 Aの分散に置き換えられないか、検討する。 投資案Cの分散の計算式を整理すると、 1(4-16)+(10-16)+(22-16)+(28-16) × 0.25 =[12 (2-8)1 +12 (5-8)1²+12 (11-8)1²+12 (148)2] x 0.25 = 2² 1(2-8)1²+(5-8) + (11-8) +(148)²1 x 0.25 =4×投資案Aの分散
となり、投資案投資案Cの標準偏差 =√4×投資案Aの分散
Aの分散を4倍したものが投資案Cの分散になることがわかる。また、 標準偏差は分散の平方根をとった値なので、
=2×投資案Aの標準偏差
となり、 投資案Cの標準偏差は投資案Aの2倍となる。
解テク
電卓を使用できない本試験で、工の標準偏差の値を計算した受験者は皆無であったと 思われる。やみくもに標準偏差の計算に時間をかけるべきでない。 本間は選択肢アから ウを検討して、消去法で解答すべき問題である。
過去類出問題
平成27年度 第17間 平成26年度 第17 平成24年度 第19


第14問
加重平均資本コストWACCの計算手順に関する次の記述について、下記の設問に答えよ。
加重平均資本コストは、株主資本-自己資本/コストと他人資本コストを、その
A に応じて加重平均することで求められる。加重平均に用いるのは、理論的にはそれぞれの B である。
また、他人資本コストには C を考慮する必要がある。具体的には、他人
資本コストに D を乗じることで、 C を考慮した他人資本コストを
求める。
(設問1)
記述中の空欄AおよびBにあてはまる語句の組み合わせとして最も適切なものはどれか。
ア A:運用形態 B:時価
イ A:運用形態 B:簿価
ウ A:資本構成 B:時価
エ A:資本構成 B:簿価
オ A:調達源泉 B:簿価
(設問2)
記述中の空欄CおよびDにあてはまる語句の組み合わせとして最も適切なもの
はどれか。
ア C:節税効果 D: 1-限界税率
イ C:節税効果 D:限界税率
ウ C:レバレッジ効果 D: 1-限界税率
エ C:レバレッジ効果 D: 1+限界税率
オ C:レバレッジ効果 D:限界税率

加重平均資本コスト (WACC) の計算手順に関する問題である。 基本的な答できる。必ず正解したい。
加重平均資本コストは、以下の計算式で求める。
WACC=
E
x株主資本コスト+ E+D
知識で解
D
x負債コストX (1-t)
E+D
※ 株主資本 (白己資本) の時価. D 負債(他人資本)の時価、t税率
この計算式に基づいて、 空欄に当てはまる語句の組合せを選択する。 1) ウ
加重平均資本コストの計算には、 株主資本 (自己資本) と負債 (他人資本) の時価の 資本構成 (割合) を用いる。 よって、空欄 A は「資本構成」 空欄 Bは「時 価」 となる。
(設問2) ア
他人資本、 すなわち負債には節税効果があるので、 加重平均資本コストの計算には税 引後の他人資本コストを用いる。 よって,空欄 C ] は 「節税効果」 空欄 [ D は 「1-限界税率」となる。
過去出問題
平成27年度 第14問 平成25年度 第14問 平成24年度 第16間 平成23年度 第16
(
第14問

第13問
企業買収に関する略語の説明として最も適切なものはどれか。
ア KPI とは、同業他社の株価を参照することを通じて買収価格を決定したうえで、経営権の取得等を行うことである。
イ LBO とは、従業員が資金を出し合って、経営権の取得等を行うことである。
ウ MBO とは、金融機関が自身の資金によって経営権の取得等を行うことである。
エ TOB とは、不特定多数の者に対し、証券市場以外の場における株券の買付け等の勧誘を通じて経営権の取得等を行うことである。

第13問 エ
企業買収に関する略語の問題である。 テキストが押さえられていれば、イ、ウが誤り で工が正答だと気付くはずである。 これを機に、解けるようにしておきたい ア 不適切である。 KPIは、 Key Performance Indicators の略である。 組織や事業 業 務の目標の達成度合いを測る定量的な指標のことで、重要業績評価指標などと訳される。 イ不適切である。 LBOは、 Leveraged Buy-Out の略である。 買収対象企業の資産や将 来キャッシュ・フローを担保として借入金を調達し、その資金で経営権の取得等を行う ことである。 なお、 従業員が資金を出し合っ
て、 経営権の取得等を行うことをEBO (Employee Buy-Out) という。 ウ不適切である。 MBO
は、Management Buy-Out の略である。 企業の経営陣が株主か ら自社の株式を譲り受けて、経営権の取得等を行うことである。 エ最も適切である。 TOBは、 Take-Over Bid の略である。 不特定多数の株主から証券 市場外で株式等を買い集める行為である。 企業買収や子会社化など、 第三者が対象企業 の経営権の取得等を目的に実施することが多い。


第12問
資本資産評価モデルCAPMに関する下記の設問に答えよ。
(設問1)
資本資産評価モデルを前提とした場合の記述として、最も適切なものはどれ か。
ア β=-1である資産を安全資産と呼ぷ。
イ β=1であるリスク資産の期待収益率は、市場ボートフォリオの期侍収益率と同じである。
ウ β=2であるリスク資産の予想収益率の分散は、β=1であるリスク資産の予想収益率の分散の2倍である。
エ 市場ポートフォリオのリターンが正のとき、β=0.5であるリスク資産の価格が下落することはない。
(設問2)
資本資産評価モデルを前提とした場合、以下の資料に基づく株式の期待収益率として最も適切なものを、下記の解答群から選べ。
資 料
市場ポートフォリオの期待収益率:8 %
無リスク資産の期待収益率:3 %
β:1.4
実効税率:40 %
解答群
ア 4.4 %
イ 7 %
ウ 10 %
エ 11.2 %

第 12 問 解説
資本資産評価モデル (CAPM)に関する問題である。 本園では、 CAPM理論の公式を使いこなせれば解答できる。 CAPM理論の公式は 以下のとおりである。
個別証券の期待収益率
=リスク・フリー・レート
+個別証券のβx (市場ポートフォリオの期待収益率ーリスク・フリー・レート)
(設問1) イ
試算が必要になるが、 CAPM理論の公式に当てはめれば正答できる。 これを機に、 解けるようにしておきたい。
ア 不適切である。 8=0である資産を安全資産と呼ぶ。 8 (ベータ) は、 市場全体の収 益率の動き (市場動向) に対し、個別証券 (リスク資産) の収益率がどれだけ動くかを 表す値である。 安全資産の期待収益率は、リスク・フリー・レートという一定の値であ り、市場動向の影響をまったく受けない。したがって、安全資産の8は0である。 なお、 =-1の個別証券は、市場ポートフォリオと正反対の動きをする。 イ 最も適切である。 CAPM理論の公式にβ=1 を代入すると、 個別証券の期待収益率
フリー・レート +市場ボートフォリオの期待収益率ーリスク・フリー・レート 市場ポートフォリオの期待収益率 となり、 個別証券の期待収益率と市場ポートフォリオの期待収益率は一致する。 不適切である。 8の
=リスク・
ウ 公式は、以下のとおりである。
p×個のα B
市の
※p (ロー) 個別証券と市場ポートフォリオの相関係数 個の。 (シグマ) 個別証券の標準偏差 市の。 (シグマ) 市場ポートフォリオの標準偏差
個別証券 (リスク資産) の分散を求めるには、この公式の両辺を2乗すればよい。
2×個の
市の
-
x個別証券の分散
市場ポートフォリオの分散
この両辺に、
市場ポートフォリオの分散
P
個別証券の分散=
を掛けると、
市場ポートフォリオの分散×B2
P
と変形できる。 この式に、 β=1 を代入すると、
個別証券の分散
市場ボートフォリオの分散×1
P
となる。 同様に、β=2 を代入すると、
個別証券の分散=
市場ポートフォリオの分散
となる。これらを比較すると、 β=2のときの分散はβ=1のときの4倍となる。 エ 不適切である。 B は、 個別証券 (リスク資産) の価格の動きの大きさが市場ポートフォ リオの価格の動きに比べて大きいか小さいかを示す指標である。 が 0.5 というのは、 リスク資産の価格が市場ポートフォリオの価格の動きの5割方、小さく動く傾向がある ことを意味している。 小さいとはいえ、価格が動くということは、価格が上昇したり下 落したりすることなので、 下落しないとはいえない。
テク
選択肢ウは検討に時間がかかるので、 先に他の選択肢を検討すべき問題である (選択 肢イが正しいと判断できれば、選択肢ウを検討する必要はない)。 (設問2) ウ
CAPM理論の公式を利用した計算問題である。 基本的な知識で解答できるので、 必 ず正解したい。 【資料】 の数値をCAPM理論の公式に当てはめると、次のようになる。 株式の期待収益率
=無リスク資産の期待収益率3% +81.4
× (市場ポートフォリオの期待収益率 8%-無リスク資産の期待収益率3%) = 10 (%)
よって、 ウが正解である。
変動性 (リスク) 確実に押さえておきたい。
B 収益率の変動性(リスク) 市場ポートフォリオよりも個別証券のほうが大きい a=1 市場ボートフォリオと同じ 0

第11問
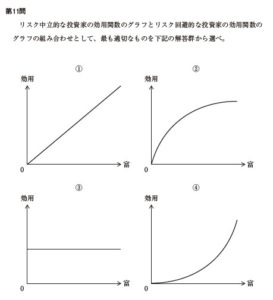
リスク中立的な投賢家の効用関数のグラフとリスク回避的な投賢家の効用関数のグラフの組み合わせとして、最も適切なものを下記の解答群から選べ。
〔解答群〕
ア リスク中立的な投資家:①リスク回避的な投資家:②
イ リスク中立的な投資家:①リスク回避的な投責家:③
ウ リスク中立的な投資家:①リスク回避的な投資家:④
エ リスク中立的な投資家:③リスク回避的な投資家:②
オ リスク中立的な投資家:③リスク回避的な投責家:④

第11問 ア 解説
投資家のタイプと効用関数に関する問題である。 グラフの縦軸 横軸ともに、 テキス ト掲載のものとは異なるため、 悩んだ受験者も多かったと思われる。 ただ、 ③のグラフ は 「富がいくら増えても効用が大きくならない」 ということを示している。 どんな投資 家であろうと、その目的は富を増やして効用を大きくすることなので、これは不適切で ある。したがって、消去法によりアとウの2択にまでは絞り込める。 まず、下の例題を考えてほしい。
(例題) あなたならどちらを選びますか? A: 確実に50万円もらえる。
BI 1/2の確率で100万円もらえるが、
1の確率で1円ももらえない。
たいていの方は、 Aを選ぶのではないだろうか。 Aを選んだあなたは、リスク回避な投資家である。 きっと、 「1円ももらえないリスクを負うくらいなら、確実に50もらえたほうがうれしい」と考えたはずだ。
反対に、「リスクを負ってでも100万円がほしい」と考えてBを選んだあなたは、リ スク愛好的な投資家である。 また、「確率的にはどちらも50万円もらえそうだから、A・ Bどちらでも同じ」と考えた方は、リスク中立的な投資家である。
では、先にリスク中立的な投資家について検討する。 リスク中立的な投資家は、リス クの大小に関係なく、 リターンの大小だけで効用が決まる。 本間に置き換えれば、 「雷
的 万円が大きいほど効用は大きく、雷と効用は比例関係にある」といえる。
たとえば、 確実に50万円もらえるときの効用をu (50) 確実に100万円もらえると きの効用を (100) 1円ももらえないときの効用を0とする。 このとき、富と効用の 関係は下記のような右上がりの直線で表せる。
u (100) u (50) u (50)- (100) 50 100
ゆえに、リスク中立的な投資家の効用関数のグラフは①である。 なお、 比例関係にあ るため、もらえる金額が半分になれば、 効用も半分になる。 したがって、
1 u (50) = ễ u (100) 2
と表現できる。
次に、リスク回避的な投資家について検討する。 リスク回避的な投資家は、 リターン 同じならリスクが小さいほうを選ぶ。 実際、以下に示すように、リターン (期待収益 )は同じだが、リスク (分散) はBのほうが大きいため、Aを選択する。 Aの期待収益率=50×1
=50 (万円)
Bの期待収益率= 100 × 12/28+0x12/2 =50(万円) Aの分散= (50-50) ×1
Bの分散 = (100-50²×1123+ (0-50)×1/12
= 2,500
続いて、 富 (収益)と効用の関係を考える。 上記と同様、 確実に50万円もらえると 用 確実に 100万円もらえるときの効用を (100) 1円ももらえな (50) いときの効用を0とする。 このとき、 Aの効用とBの効用はそれぞれ、
が率
Aの効用 (50)
Bの効用= (100)x
(100) a
と表せる。 リスク回避的な投資家の場合、
Aの効用> Bの効用
u (50)>
(100)
2
という関係にあるため、富と効用の関係は、下記のような上に凸の曲線で表せる (破線 はリスク中立的な投資家のグラフ)。 これは、 本間②のグラフにほかならない。
(100) (50)> (100) (50) 12/21(100) 富(万50 100
よって、アが正解である。
円)
ちなみに前述のとおり、リスク愛好的な投資家はリスクを負ってでも100万円を得 ようとするので、 B を選択する。 したがって、
Aの効用
平成25年度 平成23年度 第19周 第18周