
第11問
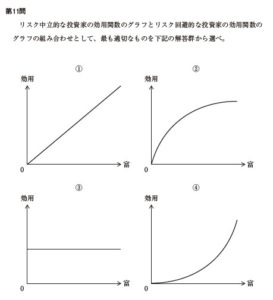
リスク中立的な投賢家の効用関数のグラフとリスク回避的な投賢家の効用関数のグラフの組み合わせとして、最も適切なものを下記の解答群から選べ。
〔解答群〕
ア リスク中立的な投資家:①リスク回避的な投資家:②
イ リスク中立的な投資家:①リスク回避的な投責家:③
ウ リスク中立的な投資家:①リスク回避的な投資家:④
エ リスク中立的な投資家:③リスク回避的な投資家:②
オ リスク中立的な投資家:③リスク回避的な投責家:④
第11問 ア 解説
投資家のタイプと効用関数に関する問題である。 グラフの縦軸 横軸ともに、 テキス ト掲載のものとは異なるため、 悩んだ受験者も多かったと思われる。 ただ、 ③のグラフ は 「富がいくら増えても効用が大きくならない」 ということを示している。 どんな投資 家であろうと、その目的は富を増やして効用を大きくすることなので、これは不適切で ある。したがって、消去法によりアとウの2択にまでは絞り込める。 まず、下の例題を考えてほしい。
(例題) あなたならどちらを選びますか? A: 確実に50万円もらえる。
BI 1/2の確率で100万円もらえるが、
1の確率で1円ももらえない。
たいていの方は、 Aを選ぶのではないだろうか。 Aを選んだあなたは、リスク回避な投資家である。 きっと、 「1円ももらえないリスクを負うくらいなら、確実に50もらえたほうがうれしい」と考えたはずだ。
反対に、「リスクを負ってでも100万円がほしい」と考えてBを選んだあなたは、リ スク愛好的な投資家である。 また、「確率的にはどちらも50万円もらえそうだから、A・ Bどちらでも同じ」と考えた方は、リスク中立的な投資家である。
では、先にリスク中立的な投資家について検討する。 リスク中立的な投資家は、リス クの大小に関係なく、 リターンの大小だけで効用が決まる。 本間に置き換えれば、 「雷
的 万円が大きいほど効用は大きく、雷と効用は比例関係にある」といえる。
たとえば、 確実に50万円もらえるときの効用をu (50) 確実に100万円もらえると きの効用を (100) 1円ももらえないときの効用を0とする。 このとき、富と効用の 関係は下記のような右上がりの直線で表せる。
u (100) u (50) u (50)- (100) 50 100
ゆえに、リスク中立的な投資家の効用関数のグラフは①である。 なお、 比例関係にあ るため、もらえる金額が半分になれば、 効用も半分になる。 したがって、
1 u (50) = ễ u (100) 2
と表現できる。
次に、リスク回避的な投資家について検討する。 リスク回避的な投資家は、 リターン 同じならリスクが小さいほうを選ぶ。 実際、以下に示すように、リターン (期待収益 )は同じだが、リスク (分散) はBのほうが大きいため、Aを選択する。 Aの期待収益率=50×1
=50 (万円)
Bの期待収益率= 100 × 12/28+0x12/2 =50(万円) Aの分散= (50-50) ×1
Bの分散 = (100-50²×1123+ (0-50)×1/12
= 2,500
続いて、 富 (収益)と効用の関係を考える。 上記と同様、 確実に50万円もらえると 用 確実に 100万円もらえるときの効用を (100) 1円ももらえな (50) いときの効用を0とする。 このとき、 Aの効用とBの効用はそれぞれ、
が率
Aの効用 (50)
Bの効用= (100)x
(100) a
と表せる。 リスク回避的な投資家の場合、
Aの効用> Bの効用
u (50)>
(100)
2
という関係にあるため、富と効用の関係は、下記のような上に凸の曲線で表せる (破線 はリスク中立的な投資家のグラフ)。 これは、 本間②のグラフにほかならない。
(100) (50)> (100) (50) 12/21(100) 富(万50 100
よって、アが正解である。
円)
ちなみに前述のとおり、リスク愛好的な投資家はリスクを負ってでも100万円を得 ようとするので、 B を選択する。 したがって、
Aの効用
平成25年度 平成23年度 第19周 第18周




コメントフォーム