

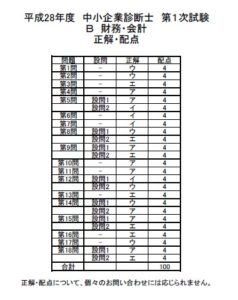
第8問
次の資科に基づいて、下記の設問に答えよ。
【資科】
第1期 第2期
期首在庫 0個 10個
生産量 110個 90個
計 110個
販売量 100個 100個
期末在庫 10個 0個
販売単価 1.000円
単位当たり変動費600円 1期当たり固定費33.000円
(設問1)
資料に関する説明の組み合わせとして、最も適切なものを下記の解答群から選べ。
a 全部原価計算を採用した場合、第1期と第2期の営業利益は同じである。
b 第1期では、全部原価計算を採用した場合の営業利益の方が、直接原価計算を採用した場合よりも大きい。
c 第2期では、全部原価計算を採用した場合の営業利益の方が、直接原価計算を採用した場合よりも大きい。
d 直接原価計算を採用した場合、第1期と第2期の営業利益は同じである。
〔解答群〕
ア aとb
イ aとc
ウ bとd
ェ cとd
(設問2)
第2期の損益分岐点比率として最も適切なものはどれか。
ア 17.5%
イ 45.0%
ウ 55.0%
エ 82.5%
直接原価計算と損益分岐点分析 (CVP分析) に関する問題である。
まず、 全部原価計算と直接原価計算の違いを簡単に確認しよう。
全部原価計算 製造原価の全部を製品単位で集計する 直接原価計算 変動製造原価のみを製品単位で集計し、 固定費は全額発生時の費用と する
第8問
全部原価計算による営業利益と直接原価計算による営業利益を比較する問題である。 難しいが、時間をかけて計算すれば正解できる。 今後も出題される可能性があるので、 得点できるようにしておきたい。
したがって、異なるのは固定費の取扱いである。 これに基づき、各営業利益を計算す ると下記のようになる。
直接原質計算 2 第1期 第2期 売上高 100,000 100,000 売土原舊 90,000 196,000 克上原圖 |固定費 |營業利益 10,000 4,000 營業利益 100,000 100,000 60,000 60,000 33,000 ,000 7,000 7.000
*各期の売上高:1,000×100個100,000 《PT》 亮上原價:下記术 夕工回在参
《全部原新計算-第1 期)
期首在車 0 販売量 100 当期投入 1600×130 -66100 生產量: 固定費 110 33,000 90,000 10 90000 期末在東 110 10 M 99,000x -9,000 110
《全部原舊計算,第2期》
期首在車 9,000 600×50 M -54,000 33.000 期首在車 10個 90個 100 044 9,000--87,000 =56,000
財務・会計
(直接原価計算・第1期>
当期投入 ・変動費 600×110 66,000 期首在庫 0個 0+66,000-66,000 100 M 66,000× 100 110 個 <- 60.000 66,000x 10 S 6,000 売上原価 110 110
〈直接原価計算・第2期 〉
6,000 販売量 6,000+54,000 10 M 100個 -60,000 「変動費 600×90 -54,000 生産量 90 |期末在庫 10個
不適切である。 全部原価計算を採用した場合、第1期の営業利益は10,000円だが、 第2期は4,000円である。
b 適切である。 第1期では、 全部原価計算を採用した場合の営業利益が10,000円 直 接原価計算を採用した場合の営業利益が7,000円となり、前者のほう
が大きい。 c不適切である。 第2
期では、 全部原価計算を採用した
場合の営業利益が 4,000円、直 接原価計算を採用した場合の営業利益が7,000円となり、後者のほうが大きい。 d適切である。 直接原価計算を採用した場合、 第1期・第2期とも営業利益は7,000円 となる。
よって、 正解はウである
解テク
各営業利益は次のような関係にある。 これを頭に入れておくと、早く解答できる。
全部原価計算の営業利益=直接原価計算の営業利益 +期末在庫に含まれる固定製造原価 一期首在庫に含まれる固定製造原価
〈第1〉
10個
期末在庫に含まれる固定製造原価=33,000 x
3,000 (PT)
期首在庫に含まれる固定製造原価0
よって、 下記のとおりに表せる。
110
全部原価計算の営業利益 = 直接原価計算の営業利益 +3,000-0
=直接原価計算の営業利益 +3,000
全部原価計算の営業利益>直接原価計算の営業利益
<第2期>
「期末在庫に含まれる固定製造原価=33,000×
0個
90 個
期首在庫に含まれる固定製造原価=第1期末在庫に含まれる固定製造原価 = 3,000 (PH)
よって、 下記のとおりに表せる。 全部原価計算の営業利益=直接原価計算の営業利益 +0 -3,000 直接原価計算の営業利益 3,000 全部原価計算の営業利益<直接原価計算の営業利益 設問2="設問2" エ="エ" 損益分岐点比率を計算させる問題である="損益分岐点比率を計算させる問題である" 基本的な知識で解答できるので必ず正解="基本的な知識で解答できるので必ず正解" したい="したい" 損益分岐点比率="損益分岐点比率" _="_" 損益分岐点売上高="損益分岐点売上高" x="x" _100="_100" 売上高="売上高" 固定費="固定費" 損益分岐点売上高円="1" 変動費率="変動費率" 限界利益率="限界利益率" 最初に="最初に" 損益分岐点売上高を求める="損益分岐点売上高を求める" _33000="_33000" _1-0.6="_1-0.6" _82500="_82500" pt="pt" 変動費="変動費" _600="_600" _0.6="_0.6" _1.000="_1.000" これを損益分岐点比率の公式に当てはめるとaztec_cursor="これを損益分岐点比率の公式に当てはめるとaztec_cursor">
(設問2) エ
損益分岐点比率を計算させる問題である。 基本的な知識で解答できるので、必ず正解 したい。
損益分岐点比率 (%) 損益分岐点売上高 x 100 売上高 固定費 損益分岐点売上高(円) = 1 変動費率 限界利益率
最初に、 損益分岐点売上高を求める。
損益分岐点売上高 33,000
1-0.6
82,500 (PT)
※変動費 600
0.6
1.000




コメントフォーム